Přehled vysokoškolských definic

Základní vysokoškolské matematické definice - přehled.

Hodnost matice

• Maximální počet LN řádků matice A se nazývá hodnost matice A.

Regulární a singulární matice

• Regulární matice - Čtvercová matice, která má LN řádky

• Singulární matice - Čtvercová matice, která má LZ řádky

Jordanova metoda

• Matici převedu na jednotkovou matici, řešením je vektor, jehož čísla jsou v sloupci pravých stran.

Lineární kombinace vektorů

• Říkáme, že vektor x je lin. kombinací vektorů x₁…..x_r jestliže existují reálná čísla c₁…..c_r taková, že platí: x=c₁x₁+ c₂x₂+…+ c_rx_r.

• Reálná čísla c₁…..c_r se nazývají koeficienty lineární kombinace. Pokud všechny koeficienty lineární kombinace jsou rovny nule, hovoříme o tzv. triviální lineární kombinaci

Lineární závislost a nezávislost vektorů

• Vektory x₁, ..., x_r se nazývají LZ, jestliže existuje jejich netriviální LK, která je rovna nulovému vektoru, tj. jestliže existují reálná čísla c₁,...,c_r , z nichž je alespoň jedno různé od nuly
• v opačném případě jsou LN
• postačující podm: Vektory x₁, ..., x_r jsou LZ tehdy a jen tehdy, když alespoň jeden z nich je LK ostatních

Frobeniova podmínka

• Soustava lineárních rovnic má řešení tehdy a jen tehdy, když hodnost matice soustavy je rovna hodnosti rozšířené matice soustavy.
• Věta o počtu řešení soustavy

• předpokládejme, že soustava lineárních rovnic má řešení, h je hodnost matice soustavy a n je počet neznámých. Potom platí:
• jestliže h = n, pak soustava má právě jedno řešení
• jestliže h < n, pak soustava má nekonečně mnoho řešení, přičemž za n-h neznámých lze volit libovolná reálná čísla a ostatní neznámé jsou určeny jednoznačně

Cramerovo pravidlo

• Mějme soustavu n lineárních rovnic o n neznámých x₁,…, x_n. Jestliže matice soustavy A je regulární, pak má soustava právě jedno řešení, které se dá zapsat ve tvaru 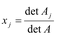, kde A_j je matice, která vznikne z matice soustavy A po náhradě j-tého sloupce sloupcem pravých stran rovnic soustavy.

Kolmý (ortogonální vektor)

• Vektory jsou k sobě navzájem kolmé, je li jejich skalární součin roven O
  

Homogenní soustava lineárních rovnic a její řešitelnost

• Soustava s nulovými pravými stranami.
• Homogenní soustava má vždy řešení pokud - h = n → Jedno řešení a to „triviální“

- h < n → ∞ mnoho řešení a to „triviální“ řeš. a ∞ mnoho řešení „netriviálních“ (pokud se alespoň jeden prvek ≠ 0)

Spojitost funkce

 

• Nechť funkce f je definována v okolí bodu c. Říkáme, že funkce f je spojitá v bodě c, jestliže pro každou posloupnost (x_n) obsaženou v D(f) platí: když x_n c, pak f (x_n) f(c)

Bolzanova věta

• Je-li funkce f spojitá v intervalu <a,b> a f(a) * f(b) < 0, pak existuje c ϵ (a,b) takové, že f(c) =0

Weierstrassova věta

• Funkce spojitá v uzavřeném intervalu <a,b> má v tomto intervalu maximum i minimum.

Derivace funkce v bodě c

• Nechť funkce f je definována v okolí bodu c. Číslo f´(c), definované vztahem f´(c) =
• 
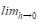
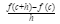
• Derivace funkce v bodě c je vlastní, když je funkce f spojitá v bodě c.

• Výsledkem vlastní derivace je reálné číslo

Extrémy funkce

• Je maximum nebo minimum funkce vzhledem k množině.
• nechť M je podmnožina definičního oboru funkce f. Jestliže pro všechna x ϵ M platí f(x) ≤ f(c) říkáme, že funkce f má v bodě c maximum na množině M, resp. f(x) ≥ f(c) říkáme, že funkce f má v bodě c minimum na množině M.
• M je okolí bodu c » lokální extrém, M = D(f) » absolutní extrém

Věta o významu 1.derivace pro průběh funkce

• Nechť f je spojitá funkce v intervalu J. Jestliže f´(x) >0 → pak je funkce f v intervalu J rostoucí < 0 → pak je funkce f v intervalu J klesající

Věta o významu 2.derivace pro průběh funkce

• Nechť f je spojitá funkce v intervalu J. Jestliže
  • f´´(x)>0 ve vnitřních bodech x ϵ J, pak je funkce konvexní v intervalu J

• f´´(x)<0 ve vnitřních bodech x ϵ J, pak je funkce konkávní v intervalu J

Newtonův určitý integrál, jeho geometrická interpretace

• Nechť k funkci f existuje v intervalu <a,b> primitivní funkce F. Reálné číslo 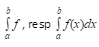definované vztahem 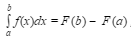, se nazývá Newtonův určitý integrál funkce f od a do b.

• Geometrická interpretace

• Je-li funkce f v intervalu <a,b> spojitá a nezáporná, pak určitý integrál 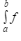 je roven obsahu plochy omezené grafem funkce f, osou x a přímkami x=a, x=b

• Věta o aditivitě určitého integrálu

• Jestliže existuje integrál

Nevlastní integrál

• Integrál, kde není funkce v jednom z krajních bodů intervalu definována.
• Nechť funkce f není v bodě a definována (resp. a= -∞) a v intervalu (a,b> k ní existuje primitivní funkce. Integrál   nazývá nevlastní integrál funkce f vlivem dolní meze.

Limita posloupnosti

• Říkáme, že posloupnost (a_n) má limitu a ϵ R*, jestliže v každém okolí bodu a leží všechny členy posloupnosti a_n od jistého indexu n₀ počínaje

Limita funkce

• Nechť funkce f je definována v prstencovém okolí bodu c ϵ R*. Říkáme, že funkce f má v bodě c limitu a ϵ R*, jestliže pro každou posloupnost (x_n) obsaženou v D (f) - {c} platí:

• když x_n c, pak f (x_n) a
• Skutečnost, že funkce f má v bodě c limitu a značíme: